近日,数学系盛万成教授黎曼双曲(非线性偏微分方程)团队在高维气体动力学拟定常流、血液流动力学理论及数值计算等方面的研究取得重要进展。
成果一、气体绕尖角处的拟定常流动,以“Two-Dimensional Pseudosteady Flows Around a Sharp Corner”为题发表在《Archive for Rational Mechanics and Analysis》(赖耕,盛万成, 2021)上。气体绕流问题一直是飞行器高超声速飞行的重要课题,有许多关键理论和技术问题亟待解决。该成果给出了气体绕楔形尖角物体流动的精细数学刻画,具有重要的理论和实际意义。
论文链接:https://link.springer.com/article/10.1007%2Fs00205-021-01665-0
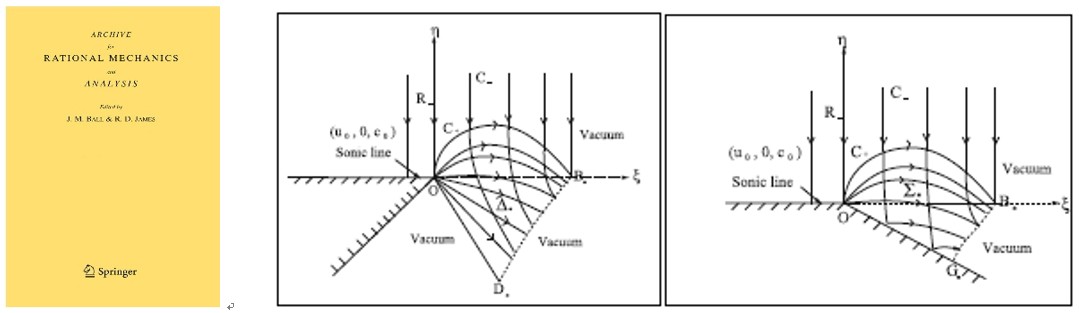
成果二、气体动力学欧拉方程基于广义黎曼问题的随机选取法,以“A Random Choice Method based on the Generalized Riemann Problem for the Euler equations in gas dynamics”为题发表在《Journal of Computational Physics》(张青龙,盛万成*,2021)上。广义黎曼问题的数值方法至今仍是一个具有挑战性的课题。该论文对一维可压缩流体动力学欧拉方程的这两种著名格式(GRP格式和RCM格式)进行了综合。这是首次实现了将两种完全不同的格式结合起来以得到精确的有限体积格式,具有非常清晰的间断分辨率的潜力。
论文链接:https://www.sciencedirect.com/science/article/pii/S0021999121003260?via%3Dihub
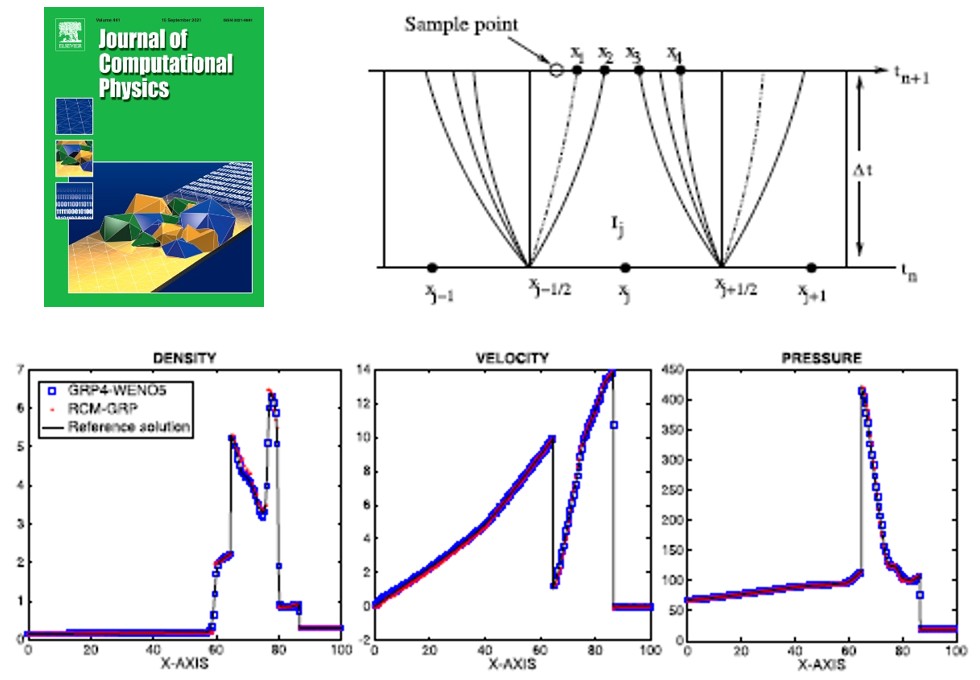
成果三、动脉血液流模型的直接欧拉GRP格式,以“A Direct Eulerian GRP Scheme For s Blood Flow Model in Arteries”为题发表在《SIAM Journal on Scientific Computing》(盛万成, 张庆龙, 郑玉玺,2021)上。该论文研究了动脉血液流动模型的数值解。针对动脉血液流动模型,开发了GRP(广义黎曼问题)格式,为研究非线性双曲问题的高阶数值模拟做出了重要的贡献。
论文链接:https://epubs.siam.org/doi/abs/10.1137/19M1284476
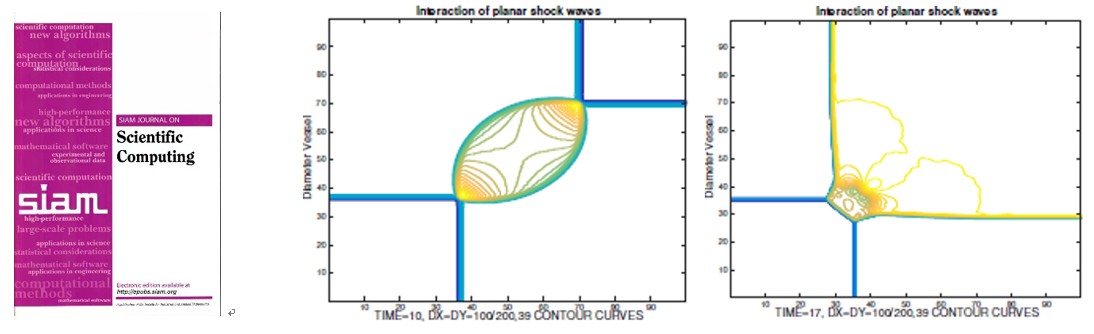
以上成果的作者中赖耕和张青龙都是盛万成教授的博士生。
本研究得到国家自然科学基金项目No. 12071278.、11371240、11771274等科研项目的资助。
盛万成教授黎曼双曲团队长期从事非线性偏微分方程理论和数值计算的研究,取得了一系列原创性的创新成果,具有鲜明研究特色,在国内外有一定的影响,2015年获上海市自然科学二等奖。培养了一批非常出色的卓越创新人才,数学系赖耕副教授就是其中的杰出代表。赖耕博士本硕博都毕业于永利数学系,在复旦大学数学科学学院博士后出站后回到永利工作。赖耕博士在非线性双曲守恒律方程组二维黎曼问题、激波反射中的von Neumann悖论、绕拐角的流动问题、超声速射流等方面取得一系列重要结果,已在《Arch. Ration. Mech. Anal.》、《J. Math. Pures Appl.》、《Indiana Univ. Math. J.》、《SIAM J. Math. Anal.》、《SIAM J. Appl. Math.》、《J. Diff. Equ.》等应用数学著名期刊上发表11篇学术论文。
黎曼双曲团队近期荣获永利首届研究生“卓越导学团队”提名奖。